A while back, risk parity was all the rage among institutional investors. And now, thanks to a raft of mutual funds floated over the past five years, retail investors are able to tap into the strategy.
What’s risk parity? Put simply, it’s a portfolio allocation tactic designed to limit risk by overweighting lower-volatility assets. You can see the appeal of this approach to endowments and foundations. These institutions have to conserve capital in perpetuity. Volatility, especially the kind seen in the wake of the Great Recession, can be crippling.
But only one kind of volatility is really bad—the downside kind. Upside volatility, you’d think, ought to be welcomed. And therein lies the problem with risk parity: An asset that is falling lower in price, as long as it exhibits low volatility, is likely to be deemed safer than a more volatile investment persistently trending upward. In essence, the model—with its exclusive focus on risk—ignores returns. At least in the near term.
For most risk-parity models, allocation decisions are based on comparisons of portfolio assets’ standard deviations. Since stocks typically are more volatile than bonds, allotments to equities in a risk-parity portfolio tend to be smaller than fixed income—the exact opposite of the classic 60-40 asset mix (a portfolio made up of 60 percent stocks and 40 percent bonds). Over the past five years, that approach has proven costly.
Here’s why: The “parity” in the model means the allocation of the low-volatility asset is raised to equal the effective risk of the high-volatility asset. Suppose, for example, we want to build a simple two-asset portfolio consisting of the SPDR S&P 500 ETF (NYSE Arca: SPY) and the iShares Core US Aggregate Bond ETF (NYSE Arca: AGG) representing broad market exposure to domestic equity and fixed-income securities. If recent history shows SPY’s standard deviation at 18 percent and AGG’s at 4 percent (much as it was five years ago), we’d make our initial equity allocation thus:
Ws = σa/(σs+ σa)
where, Ws = weight of SPY allocation;
σa = standard deviation of AGG;
and σs = standard deviation of SPY.
AGG’s weight can then be determined simply by subtracting Ws from 100 percent. By this method, a risk-balanced portfolio could have been constructed five years ago with an 18 percent allocation to SPY and an 82 percent commitment to AGG.
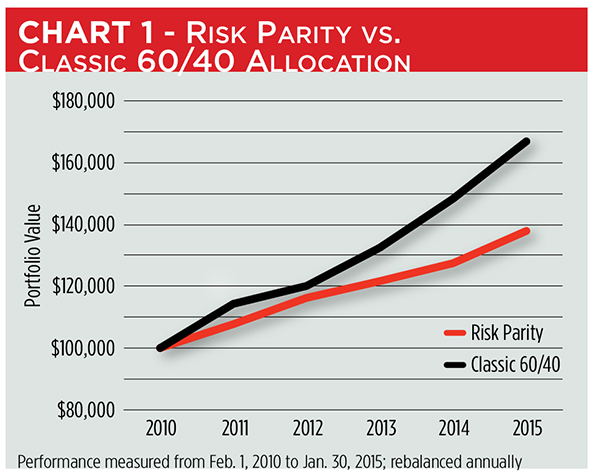
So where’s the cost in this? It becomes apparent if you compare the portfolio’s value over the ensuing five years to a classic 60-40 portfolio. When rebalanced annually (the classic portfolio to its 60-40 norm and the risk-parity portfolio to an allocation based on each preceding year’s standard deviations), the risk-parity portfolio’s cumulative gain falls far short of the profit made by classic reallocation. Chart 1 illustrates how a $100,000 investment might have grown utilizing each rebalancing approach. Over five years, risk parity produced a 38 percent gain while a 60-40 allocation generated a 67 percent profit.
The Role of An Allocation Strategy
The cost of allocating our two-asset portfolio by a risk-parity formula was nearly 29 percent over five years or, on average, 6 percent per year. Given this, you may well ask what’s so smart about risk-parity investing. That’s the very question posed—and answered—by UBS Global Research strategists Stephane Deo and Ramin Nakisa in a recent white paper entitled “Weight Watcher.”
The role of an allocation strategy, according to Deo and Nakisa, should be to maximize returns, not just to minimize risk. They don’t dismiss risk management out of hand, though. Instead, they propose basing allocation decisions on risk-adjusted returns measured by the Sharpe ratio.
Named for its creator, Nobel laureate William Sharpe, the ratio divides an asset’s gain or loss (above or below the risk-free rate of return) by its standard deviation. Using the Sharpe ratio as an allocation determinant places more emphasis on assets with the potential for greater returns.
By substituting Sharpe ratios for standard deviations in our weighting formulae, we could have initiated our two-asset portfolio with a 53 percent allocation to SPY, offset with a 47 percent weighting in AGG. Rebalancing the portfolio annually with the current Sharpe ratio yields a five-year cumulative gain of 41 percent, incrementally better than the risk-parity model but far short of the gain realized with the classic 60-40 apportionment.
We can take Deo’s and Nakisa’s notion of risk management a step further by using Sortino ratios instead of Sharpe ratios to balance our portfolio allocations. The Sortino metric uses downside deviation rather than standard deviation to score risk-adjusted returns. In essence, the Sortino ratio penalizes an investment for bad volatility, not good volatility. For a given asset, Sharpe and Sortino ratios will be fairly close to one another when return distributions are symmetrical. As distributions skew to one side or the other (positively or negatively), the ratios will diverge.
For example, the initial Sharpe ratio for SPY was 1.82 while the ETF’s Sortino ratio was 1.13. (Higher or more positive values for both metrics represent greater returns per unit of risk.) AGG’s ratios were far more disparate, with a Sharpe value of 1.70 and a 3.92 Sortino reading. The difference can be explained by AGG’s consistent uptrend: There was much less downside deviation in the bond fund’s track record compared to SPY’s.
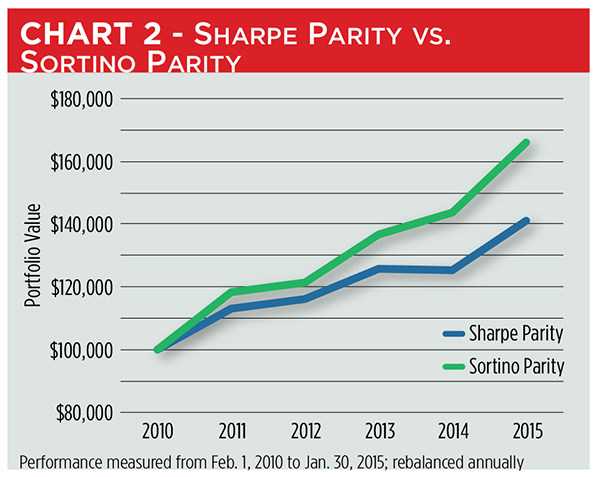
Plugging Sortino ratios into our equation yields initial weightings of 86 percent for SPY and 14 percent for AGG. Through annual rebalancing, our portfolio would have grown 66 percent over five years, far more than the Sharpe parity model and on par with the classic 60-40 paradigm.(See Chart 2.)
A Fair Degree of Variability
These four allocation schemes present distinct management challenges. For sheer simplicity, of course, the classic 60-40 model can’t be beat. No advanced math is required to rebalance the portfolio, and the allocation sizes are easily remembered.
In contrast, you’ll need some algebra and some statistical savvy to come up with parity-based allocations. There’s a fair degree of variability, too, in the size of those allocations from year to year.
The Sharpe parity model seemingly produced the most even-handed allocations (see Table 1), but there’s a lot of variance embedded in the average number. In 2013, for example, the model called for a 100 percent allocation to bonds, a setup that offset a 96 percent allocation to stocks in 2011.
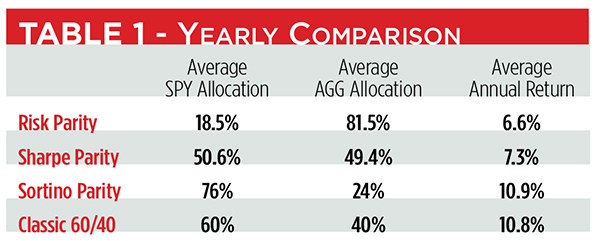
The opposite tack was seen in the Sortino-based portfolio. In every year but one (2013), stocks were overweighted. Yearly returns swung between 18 and 3 percent.
The most consistent model was the risk-parity scheme. Its allocation to bonds was unswervingly large every year. However, the price for such constancy was a mediocre, albeit relatively stable, yearly return.
From this admittedly simple study with a relatively short time frame, we see it’s possible for investors and their advisors, depending on their mathematical sophistication, to build parity-based portfolios of their own. A number of pathways are open to manage risk at a modest cost. The expense for holding the two-asset mix is just 9 basis points (0.09 percent) annually. That’s vastly cheaper than risk-parity mutual funds, which sport an average expense ratio of 105 basis points.
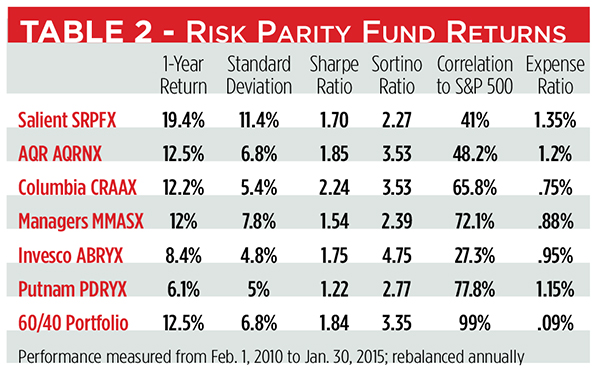
You can only get risk parity out of these mutual funds, too. To date, no Sharpe- or Sortino-based portfolios have been launched. That goes a long way, perhaps, in explaining their recent track records. Only one fund, the Salient Risk Parity Fund (OTC: SRPFX) bettered the return of a 60-40 portfolio over the past year. (See Table 2.)
So, are parity-based portfolios worth their expense? From what we can see here, they’ve certainly been no bargain, at least of late. Would risk parity funds earn their place in a client’s portfolio should markets turn dramatically? That’s a call only investors, and their advisors, can make.


